Quantum Computing for Quantum Chemistry with qc2
Quantum Computing is a rapidly evolving field that has the potential to transform the way we approach complex computational problems. Quantum Chemistry stands out as a prime application area, with anticipated impacts ranging from the development of new materials to novel drugs.
In this blog, we introduce qc2, a user-friendly, modular software designed to seamlessly integrate traditional quantum chemistry codes with modern quantum computing Software Development Kits (SDKs).
However, despite recent advances in both hardware and software, the path to fully error-corrected, utility-scale quantum computations may still take a while. For the moment, as we navigate in the Noisy Intermediate-Scale Quantum (NISQ) era towards Quantum Utility, we need to learn how to make the most out of the available algorithms that run on as-yet error-prone, imperfect hardware: the so-called NISQ algorithms.
Unavoidably, Quantum Computing and Quantum Chemistry, and particularly their combination, demand a high level of technical knowledge. The available software packages are highly specialised, requiring users to have an excellent understanding of the fundamental concepts involved from the start. This might scare away both computational chemists and software engineers alike.
This situation has been greatly alleviated by the increasing availability of excellent educational resources and good quality open-source software, some even tailored specifically for the quantum chemistry community, e.g., Qiskit-Nature, PennyLane.qchem and Tangelo. And we believe that this is the right way forward.
Enter qc2, a user-friendly, modular software designed to seamlessly integrate traditional quantum chemistry codes with modern quantum computing SDKs. Designed with reusability and interoperability in mind, qc2 leverages popular existing tools such as the Atomic Simulation Environment (ASE) and Quantum Chemistry Schema (QCSchema). It can also be easily customized to work with your preferred backends, requiring minimal implementation effort.
Before we dive in, let’s quickly recap some useful concepts…
Quick Recap: Quantum Chemistry with Classical Computers
The primary goal of quantum chemistry is to understand the structure and properties of matter at microscopic level. Atoms and molecules are intricate quantum entities and are characterized by discrete energy levels.

Such a quantized energy spectrum naturally arises from solving the systems’ Schrödinger equation (SE):

This equation represents a typical eigenvalue problem that can only be solved exactly for one-electron systems, e.g., the hydrogen atom. For all other systems, we must rely on mathematical and physical models that approximate the exact solutions to the SE. Examples of such models are the Hartree–Fock (HF) method, Coupled cluster (CC) and Full configuration interaction (FCI).
In general, the strategy involves expanding the unknown wave function of your system as a linear combination of n known wave functions:

Now, the task of determining the coefficients α, β, γ, and δ, along with the associated ground and possibly excited-state energies, involves setting up and diagonalizing a large n by n matrix:

This step is certainly the major computational bottleneck for classical computers and the one that quantum algorithms seek to bypass.
As a general rule, the larger n is, the closer the solution approaches the exact solution to the SE, but the more computationally expensive it becomes. Not surprisingly, typical “gold-standard” methods like CCSD(T) (let alone FCI) quickly become unaffordable for medium-to-large sized molecules.
Quantum Chemistry with Quantum Computers: NISQ algorithms

Let’s now examine the problem we just discussed from a different perspective: that of Quantum Computing.
Within the NISQ era, the task of approaching the exact solution to the SE primarily relies on hybrid quantum-classical algorithms, and there are compelling reasons for this. These algorithms are designed to run on noisy quantum hardware; they utilize as few quantum gates as possible and can be optimized to operate within the limited coherence time of the devices’ qubits, the units of quantum computation. Among these, the Variational Quantum Eigensolver (VQE) is specially prominent when the goal is to calculate ground-state energies and properties of molecules.
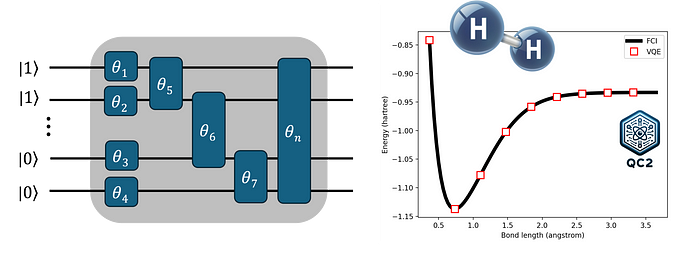
The VQE workflow (see figure above) is relatively simple to understand as it closely parallels the traditional methods based on the variational principle we previously discussed. The core of the algorithm can be broken down into the following steps:
- Reference quantum circuit. Similar to a typical quantum chemistry calculation, we begin by defining a reference wave function for the target molecule, |φ₀⟩. This is usually accomplished by using traditional quantum chemistry packages, e.g., by conducting a HF calculation with PySCF. From this, a reference quantum circuit can be created by directly mapping the spin-orbitals’ occupation numbers into initial qubit states (the calculated electron integrals are also useful later for building the molecular Hamiltonian in step 3). As an example, consider a hydrogen molecule (H₂) with a minimal basis set, such as STO-3G. Here, the final HF wave function |1100⟩ is mapped into a four-qubit quantum circuit |1⟩ ⊗ |1⟩ ⊗ |0⟩ ⊗ |0⟩. For larger molecules or one-electron bases, it may be necessary to restrict the qubit space by creating a reference quantum circuit out of a preselected active space.
- Parametrized quantum circuit. After setting the initial qubit states, the next step is to represent the wave function |Ψ₀⟩ on the quantum device, i.e., to prepare a parametrized quantum state. This is achieved by applying a predefined set of quantum gates, which depend on certain parameters θ, to the initial qubit states. Similarly to |Ψ₀⟩, the resulting parametrized quantum circuit |Ψ(θ)⟩, often referred to as the ansatz, seeks to approximate the true ground-state wave function of the target molecule. The set of variational (qubit rotation) parameters θ is, in some sense, analogous to the coefficients α, β, γ, and δ discussed earlier in the context of traditional quantum chemistry.
- Energy Estimation. With the parametrized quantum circuit at hand and a set of initial parameters θᵢ, we estimate the expectation value of the molecular Hamiltonian. This process involves mapping the Hamiltonian in second quantization into a qubit representation, namely, as a sum of Pauli terms. The final energy, which is given as a sum the measured expectation values of each Pauli term, depends on θᵢ and should be minimized accordingly.
- Classical Feedback: The minimization process is carried out using an external classical optimization routine, which updates the circuit parameters θᵢ.
- Steps 3 and 4 are repeated until convergence is achieved, resulting in the lowest possible expectation value. The final energy corresponds to the ground-state energy of the target molecule as predicted by VQE.
The quality of the VQE solutions depends on several factors, including the size of the active space (if any), type of ansatz, initial guesses for the circuit parameters, the classical optimizer used, and other potential sources of error if run on real quantum hardware.
Another popular NISQ algorithm for finding the ground-state energy of molecules is the orbital-optimized VQE (oo-VQE), which extends the traditional VQE. In oo-VQE, not only are the circuit parameters optimized, but the original HF molecular orbitals are also allowed to relax during the classical optimization process. For this reason, ground-state variational energies obtained with oo-VQE are generally lower than those from traditional VQE runs, but they are also computationally more expensive. As will be shown later, VQE and oo-VQE could be seen as some sort of quantum analogues of the traditional CASCI and CASSCF ab initio methods.
Overview of qc2
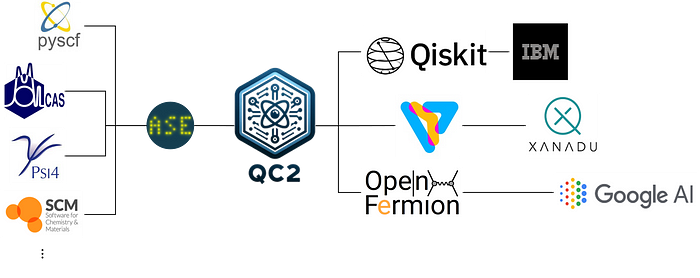
qc2 is an open-source python package specifically crafted for hybrid quantum-classical algorithms such as VQE and oo-VQE. It embraces several core design principles:
- Leveraging Existing Tools: qc2 is interoperable with existing open-source quantum chemistry tools, like ASE calculators, and adheres to standard data schemas, such as QCSchema or FCIDump. This ensures efficient data exchange necessary for various quantum computing libraries.
- Seamless Integration with Quantum Computing SDKs: qc2 is designed to work effortlessly with Qiskit and PennyLane, ensuring a smooth user experience for developers.
- Modularity: The package boasts high modularity, featuring a robust built-in algorithms package that simplifies extensions and enhancements.
- User-Friendly Design: qc2 is straightforward and has an intuitive interface, enabling users to focus on their research and applications with minimal technical details.
In the code block below, we present a minimal example using qc2 for a simple VQE run on the water molecule:
# Import ASE-related modules
from ase.build import molecule
# Import qc2 modules
from qc2.data import qc2Data
from qc2.ase import PySCF
from qc2.algorithms.pennylane import VQE
from qc2.algorithms.utils import ActiveSpace
# Instantiate qc2Data class
qc2data = qc2Data(
molecule=molecule("H2O"),
filename="h2o.hdf5"
)
# Specify and run the quantum chemistry qc2-ASE calculator
qc2data.molecule.calc = PySCF(
method="scf.RHF",
basis="sto-3g",
)
qc2data.run()
# Instantiate VQE class
qc2data.algorithm = VQE(
active_space=ActiveSpace(
num_active_electrons=(2, 2),
num_active_spatial_orbitals=4
),
)
# Run VQE algorithm
qc2data.algorithm.run()As noted, qc2 is designed around the qc2Data class, which links traditional quantum chemistry codes with quantum computing backends through custom ASE calculators and formatted data files. Here, the molecular structure of water is built from ASE’s G2 database, with the reference HF run with qc2’s custom PySCF ASE calculator. By default, all relevant electronic structure data, including the initial molecular orbitals and electron integrals, are saved in the h2o.hdf5 formatted datafile, following the QCSchema. The information contained in this file is used by qc2Data to build the molecular hamiltonian and its qubit representation. Despite being highly customizable, all the details of the VQE workflow discussed in the previous section are abstracted into a VQE class instance, which, in this case, corresponds to the PennyLane VQE class from the qc2’s algorithms package. This is passed to the qc2data.algorithm attribute.
The next example illustrates how to conduct an oo-VQE run using the Qiskit oo_VQE class as implemented in the qc2’s algorithms package:
# Import ASE-related modules
from ase.build import molecule
# Import qc2 modules
from qc2.data import qc2Data
from qc2.ase import PySCF
from qc2.algorithms.qiskit import oo_VQE
from qc2.algorithms.utils import ActiveSpace
# Instantiate qc2Data class
qc2data = qc2Data(
molecule=molecule("H2O"),
filename="h2o.hdf5"
)
# Specify and run the quantum chemistry qc2-ASE calculator.
# If you already have "h2o.hdf5" from a previous run, you can skip this step.
qc2data.molecule.calc = PySCF(
method="scf.RHF",
basis="sto-3g",
)
qc2data.run()
# Instantiate oo_VQE class
qc2data.algorithm = oo_VQE(
active_space=ActiveSpace(
num_active_electrons=(2, 2),
num_active_spatial_orbitals=4
),
)
# Run oo-VQE algorithm
qc2data.algorithm.run()The structure of the input is exactly the same as before, with the exception that we are now instantiating and running a different algorithm class. A distinct qc2-ASE calculator could also be used, such as DIRAC or your own calculator, with minimal changes and effort. This is a hallmark of qc2. Additionally, since we have previously completed a HF calculation in our VQE example above and saved all relevant ab initio data in h2o.hdf5, we could simply skip this step and proceed directly to defining the oo_VQE class. In this scenario, qc2 will automatically read the data contained in h2o.hdf5.

The figure shows the energy convergence of ground-state water as obtained using the above qc2 input examples. Although qc2 can be directly interfaced with real quantum backends, for illustration purposes, all quantum circuit evaluations were conducted with the default.qubit state simulator device for PennyLane and the Qiskit Estimator primitive with StateVector, both providing exact expectation values. As expected, oo-VQE energies are variationally lower and converge nearly exactly to the predicted CASSCF values. Recall, however, that while oo-VQE is computationally more expensive than traditional VQE, this additional burden is entirely placed on the classical computer (optimizers), not the quantum backend. Note further from the figure that, since all initial circuit (and orbital rotation) parameters are set to zero by default, both VQE and oo-VQE initiate their interactive processes at the reference HF energy.
What’s next ?
qc2 is an ever-evolving open-source project, constantly enriched by new algorithms and features. Looking ahead, we are excited about incorporating even more enhancements. We warmly welcome your contributions, whether they are new ideas, unique perspectives, or intriguing use cases you would like to see qc2 tackle. Every form of participation is valued — from a quick comment or question to in-depth pull requests. Join us in shaping the future of qc2!
This article was co-authored with Nicolas Renaud, with whom I maintained a fruitful collaboration during the QCforQC project, and who generously shared his experiences and knowledge with me.
