Masking time-series for eXplainable AI
Why did my Machine Learning (ML) model make this decision? Is it paying attention to the right elements of the data we give it?
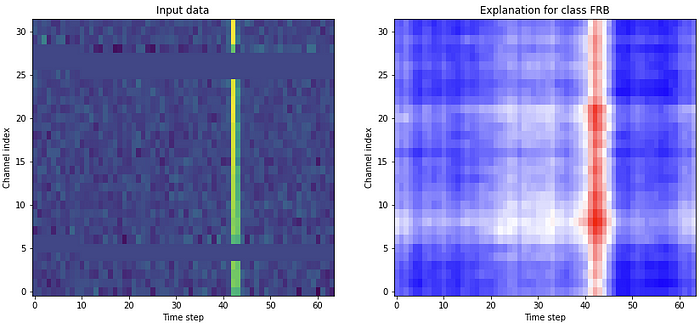
Explainable AI (XAI) methods help gain insights into the decision-making of ML models. Some XAI methods don’t require any knowledge of the inner workings of such models, which can therefore be any completely black box model. Such XAI methods work on any kind of model, any kind of classification/regression model. XAI methods of this kind, like RISE or LIME, rely on making small changes to the input data, and analyzing how the output of the model changes accordingly. This is repeated many times. The inputs and outputs of these iterations are then combined in a single attribution map summarizing what features of the input steer the model in certain directions.

For our library of XAI tools, called DIANNA, I was recently working on a new masking functionality (see Figure 2). This functionality is intended to work with time series data and exploit its general properties. The masking function should mask, or perturb, an original time-series many times. These masked time-series variants are then fed to an ML model after which the output is analyzed and combined into an attribution map. To draw valid conclusions during analyses, the masking function should have certain properties (e.g. every time step should have the same probability to be masked). On the other hand, I wanted to be able to exploit the properties commonly present in time series data, namely correlations between data in adjacent time steps.
Mask requirements
I was looking for my masking function to have the following 4 requirements:
- Mask blobs of adjacent time-steps together. The rationale behind this is that time series data is often recorded on a higher resolution than the phenomena that we want to use to predict (eg. Several days of warm weather on a day resolution time-series; multiple time steps of a certain acceleration in an accelerometer recording). In order to mask such a phenomenon from our data, we need to mask a number of adjacent time-steps.
- We want the user to be able to specify the scale of such phenomena to be masked. It is completely dataset-dependent on how many adjacent time-steps should be masked together. In some datasets, readings on many time-steps should be considered together and therefore masked together while on other datasets no such clustering should be done at all.
- We want the specified size of the clusters or blobs to vary somewhat in order to increase the span of patterns that can be masked accurately given that a large enough number of masks are used.
- We want the probability to be masked
p, for each element in the cross product of channels and time steps, to be exactly equal to a user-specified value. If this requirement is not met, XAI methods tend to produce completely invalid results.
Masking approach
I chose the following approach to generate masks for a given time-series length t and a user-defined number of features f. The number of features is the number of phenomena that the user suspects are in a time-series of length t. In general, we expect this number to be smaller or equal to the time-series length t.

M)In order to end up with a resulting mask M that satisfies requirement 1 and requirement 2, we start by creating a new fixed-interval time-series of length f (f here stands for feature length) which we call grid G. The values of the grid G are chosen randomly from a continuous uniform distribution. This generated grid G contains the pattern that we will use to base our mask M on (see step 1 in Figure 3). In order to have the mask M have length t, we project our floating point valued grid G of length f onto a new time-series of length t using linear interpolation (see step 2 in Figure 3).
We chose to generate a grid G using floating masks to create a grid with more information than a boolean mask would contain. This extra information is then used to vary the size of the blobs of adjacent masked time-steps. This helps us create a mask with requirement 3. The next step explains how this is done.
To end up with the correct number of masked elements (part of requirement 4), we now choose a threshold such that the fraction p of all time-steps is under the threshold (see step 3 in Figure 3). All time-steps below the threshold are masked while all time-steps above remain unmasked.
Loose ends
The above steps will result in masks that seemingly have all the properties that we need. However, even though the correct number of time-steps are masked to adhere to the user-specified fraction, p, not all time-steps have the same probability to be masked. This can be illustrated with an example. In Figure 4 the situation is shown when choosing the values p=1/3, f=2 and t=3. These values indicate that we want a mask of 3 time-steps that contain 2 blobs of features, so all patterns are allowed except 1 0 1 and 0 1 0, of which we want 1 time-step to be masked (on average). If we project the start and end of grid G exactly on the start and end, respectively, of our mask of length t, the value of the middle point of that mask will always be an interpolation of 2 grid points, while the first and last point of that mask will have a value based on exactly 1 of those grid points. The middle point will therefore never be the point with the highest or lowest float value and will therefore always be above the threshold and never be masked.

While the example above shows an extreme case, in order for methods like RISE or LIME to work as intended, it is necessary that we mask all time steps with equal probability (requirement 4). To ensure that it does, we come up with the following fix. Instead of projecting the first and last point in the grid G, and we take a segment of length f-1 from G to project on our mask M. This gives us room to introduce an offset between, which we can vary so every projected point is equally likely to be near the grid (see Figure 5). This results in an equal probability of masking each time step in the mask.

Try it yourself!
The ideas in this post are implemented in the mask strategies in the DIANNA code. The code contains similar solutions implemented for different data domains such as images (based on the mask strategy in the original RISE code), tabular data and text. They are all in our maskers module. DIANNA has tutorials for every data domain so it’s easy to try it out in Google Collab or on your own machine!
Acknowledgments
Thanks to Carsten Schnober and Elena Ranguelova for reviewing this text.

